Background
MMEV
For the uninitiated, a high level primer on MEV under Proof of Stake (PoS) can be found here. MMEV or multiblock MEV refers to any MEV strategy that is conducted over consecutive blocks. Multiblock MEV is not unique to Ethereum and has existed on other PoS blockchains for some time. However, it is far more relevant due the sheer volume of high value transactions taking place on Ethereum.
Proposers (a.k.a validators) with consecutive blocks can employ novel multiblock strategies. These opportunities present themselves very infrequently for the vast majority of small validators. Large pools are therefore able to earn a higher yield proportional to the size of their stake.
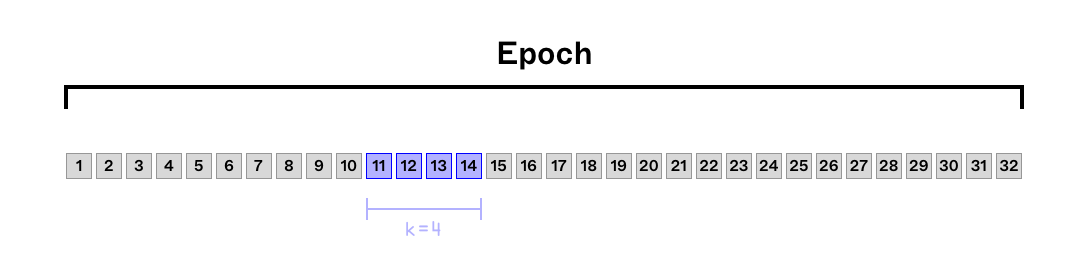 Currently, validators are able to know ahead of time whether they will have the opportunity to propose a block or consecutive blocks in addition to the identities of all other proposers in that epoch - a fundamental change from PoW.
Currently, validators are able to know ahead of time whether they will have the opportunity to propose a block or consecutive blocks in addition to the identities of all other proposers in that epoch - a fundamental change from PoW.
Validator Selection Process
Under Proof of Stake on Ethereum, time is divided into slots (lasting 12 seconds) and epochs (32 slots). The probability of a single validator being pseudo-randomly selected to be a block proposer for a given slot is inversely proportional to the number of active validators in the network at the time of selection. Given the fact that at most one validator proposes a block at any given slot, it follows that for an entity controlling multiple validators, the probability of block proposing for this entity is the summation of these individual probabilities. In other words, it is proportional to the number of validators controlled by the entity.
Problem Formalisation
Define blocktuple as consecutive blocks within the same epoch that are proposed by the same validator / entity. We will make the distinction between these where necessary. Define -blocktuple as a blocktuple with length .
Given the probabilistic nature of validator selection, one can model the various dynamics of this random process, some of which are more relevant than others. Some interesting random variables would be:
- = Number of -blocktuples, either for a single entity or across all entities and validators
- = Length of the longest -blocktuple, either for a single entity or across all entities and validators
- = Number of blocktuples, either for a single entity or across all entities and validators
- = All blocktuples having length , note that this is equivalent to
In this piece we present empirical results for all these random variables as well as theoretical results for .
Notation
- = epoch , for
- = slot , for
- = = slot j in epoch , for and
- = validator with index , for
- = block proposing validator at slot , for and
- = validator set at epoch , for
- = validator pool , for and = validators with label "others"
- = validator pool set for validator pool at epoch , for and
- = ratio of validators in validator pool at epoch , for and
- = number of -blocktuples
- = length of the longest -blocktuple
- = number of blocktuples
- = having no -blocktuple with length
- Similar to the notation defined below for , for all , , and
- = number of -blocktuples in epoch from any validator/entity
- = number of -blocktuples in epoch from validator pool (=entity)
- = number of -blocktuples in epochs to from any validator/entity
- = number of -blocktuples in epochs to from validator pool (=entity)
Theoretical Analysis
Here we describe an exact numerical solution to the cumulative distribution function (and subsequently the probability mass function) of , for the length of the longest -blocktuple in epoch from validator pool .
Definition
As presented above, the probability of block proposition by a validator pool at any slot within an epoch is equal to the ratio of the active validator set and the total number of validators controlled by the pool. One can reduce the same problem to independent coin tosses of a biased coin with probability of heads . Then, which denotes the length of the longest run of heads in these coin tosses is actually the same random variables as in the validator selection process.
Solution
Consider independent tosses of a biased coin with probabilities of heads and tails given as and . Let denote the length of the longest run of heads. Instead of focusing on probability mass function (pmf) directly, consider the cumulative distribution function (cdf) of , which is defined as .
Define as the number of sequences of length in which exactly heads occur, but at most of those occur consecutively. Then one can decompose the cdf as:
which means only is yet to be solved.
Observe that, for the general case , for any string of heads and tails that is counted within , it starts with many heads and then a tails for . Then, for , the recursive formula for can be written as:
For or , is trivial. For , is trivial. For and , is again trivial, as does not matter.
Using these observations, it is possible to implement an exact numerical solution for the cumulative distribution function (and subsequently probability mass function) of . Using the equivalence of to the random variable in the validator selection process, we end up with a numerical procedure that calculates the exact cdf (and pmf) of .
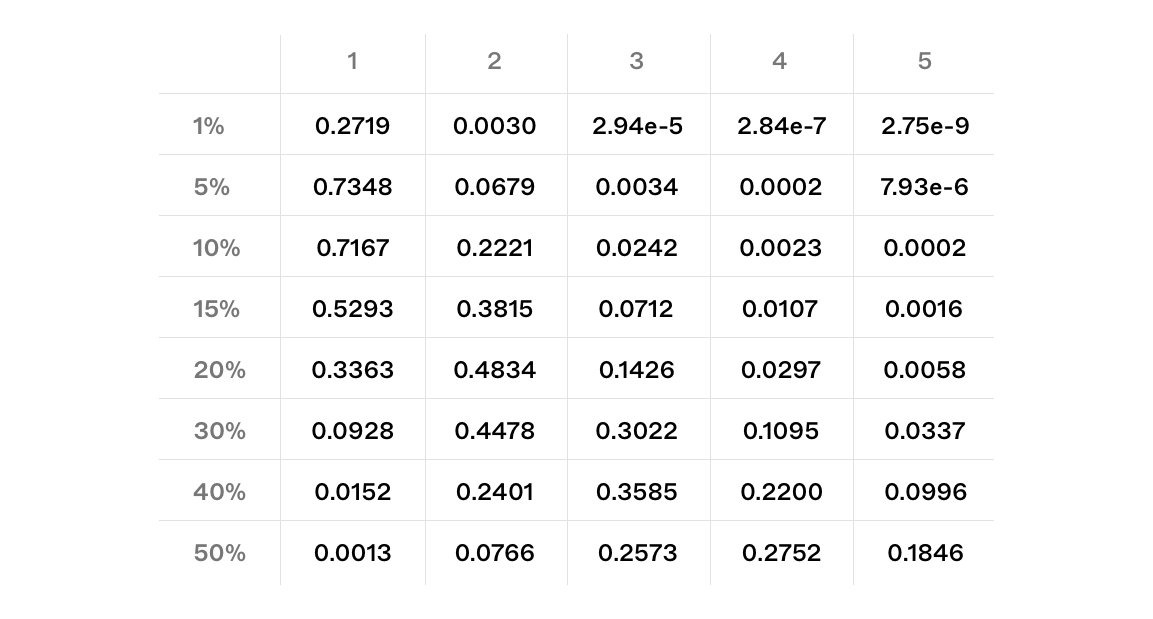
Calculated Probabilities
As presented in the previous section, it is possible to find the cdf and pmf of , the length of the longest -blocktuple in epoch from validator pool exactly. Here we calculate and present the pmf for various s and s.
Empirical Analysis
Statistical validation of our model is achieved with the Monte Carlo method. For every setting we focus on, we run simulations to study various random events related to the validator selection process.
Simulating with Static Validator Sets
First, we simulate the same setting within the theoretical analysis, one entity controlling ratio of the validators. For each value, we simulate 1,000,000 epochs, calculating every epoch. We aggregate results for across all simulations. In other words, this is the simulation of based on different values of .
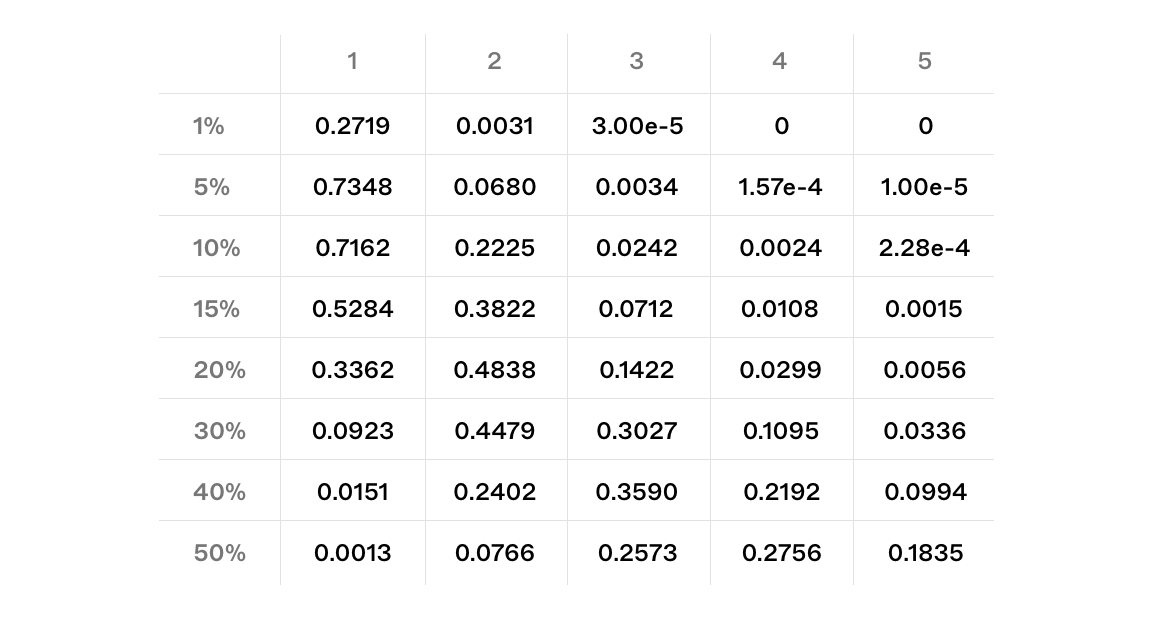
The results of our calculated probabilities closely match the simulated outputs.
Secondly, we simulate 1 day worth of epochs (=225 epochs, assuming each slot takes 12 seconds) for different values. For every simulated epoch, we calculate s and take the median across simulations to come up with the median expected number of for various values of and . In other words, this is the simulation of based on different values of .
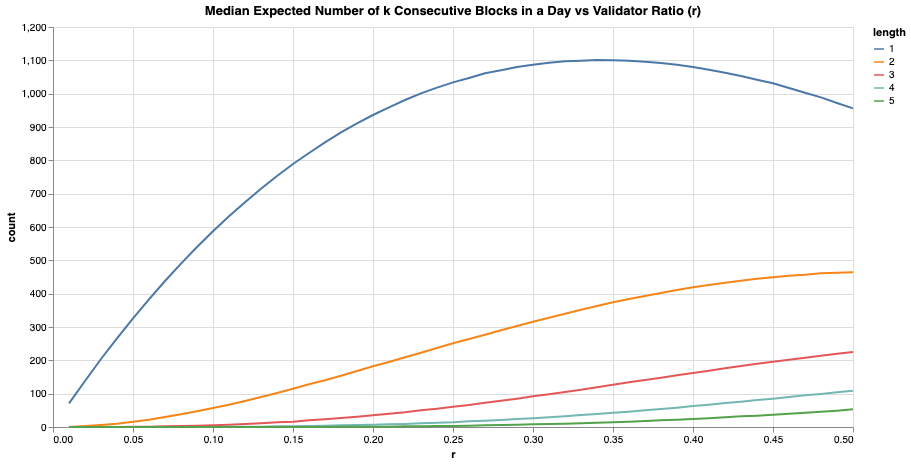
An entity with a static 15% share of the active validators () can expect to get 115 2-blocktuple and 16 3-blocktuple opportunities per day which is non trivial!
For comparison, an entity with ⅓ of the stake i.e. 5% share of the active validators () can only expect to get 16 2-blocktuple and 1 3-blocktuple opportunities per day. This example illustrates how the number of k-blocktuple opportunities are skewed towards larger validator pools.
Simulating with Dynamic Validator Sets
Observing events on the beacon chain allows us to compare our simulated results with empirical data. Rather than choosing a value arbitrarily, it is more interesting to compare simulated and empirical results for a real world entity.
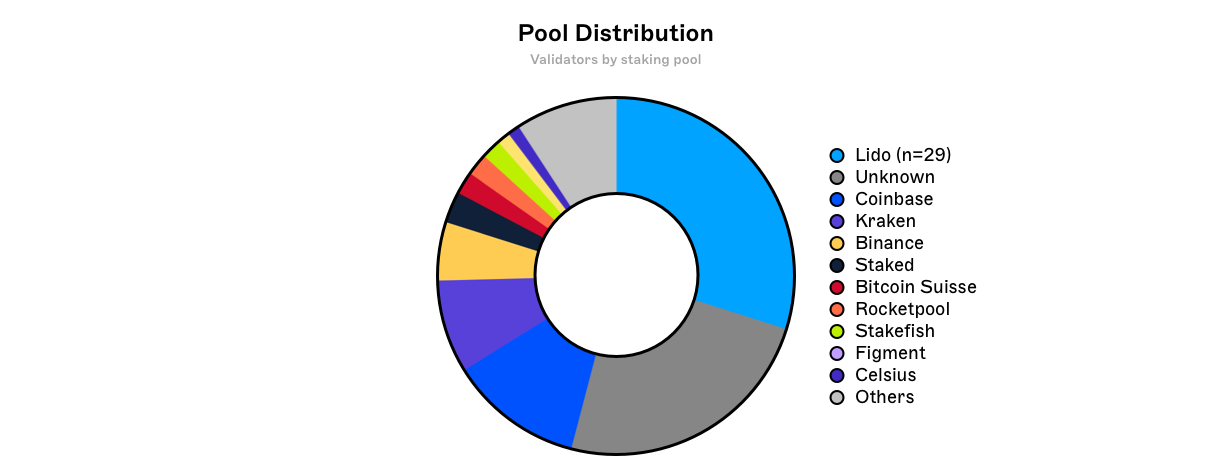
Analysing a Validator Pool
The methodology for identifying which pools a validator node belongs to varies from pool to pool. Validator pools such as Lido have clearly labelled their validators, whilst labelling others requires identifying patterns in depositing wallet flows amongst other things - which inevitably requires certain assumptions to be made.
For simplicity, we have selected Kraken which has 1 beacon chain depositor address. This address either deposits directly to the beacon deposit contract, or uses an intermediary smart contract which facilitates batch deposits.
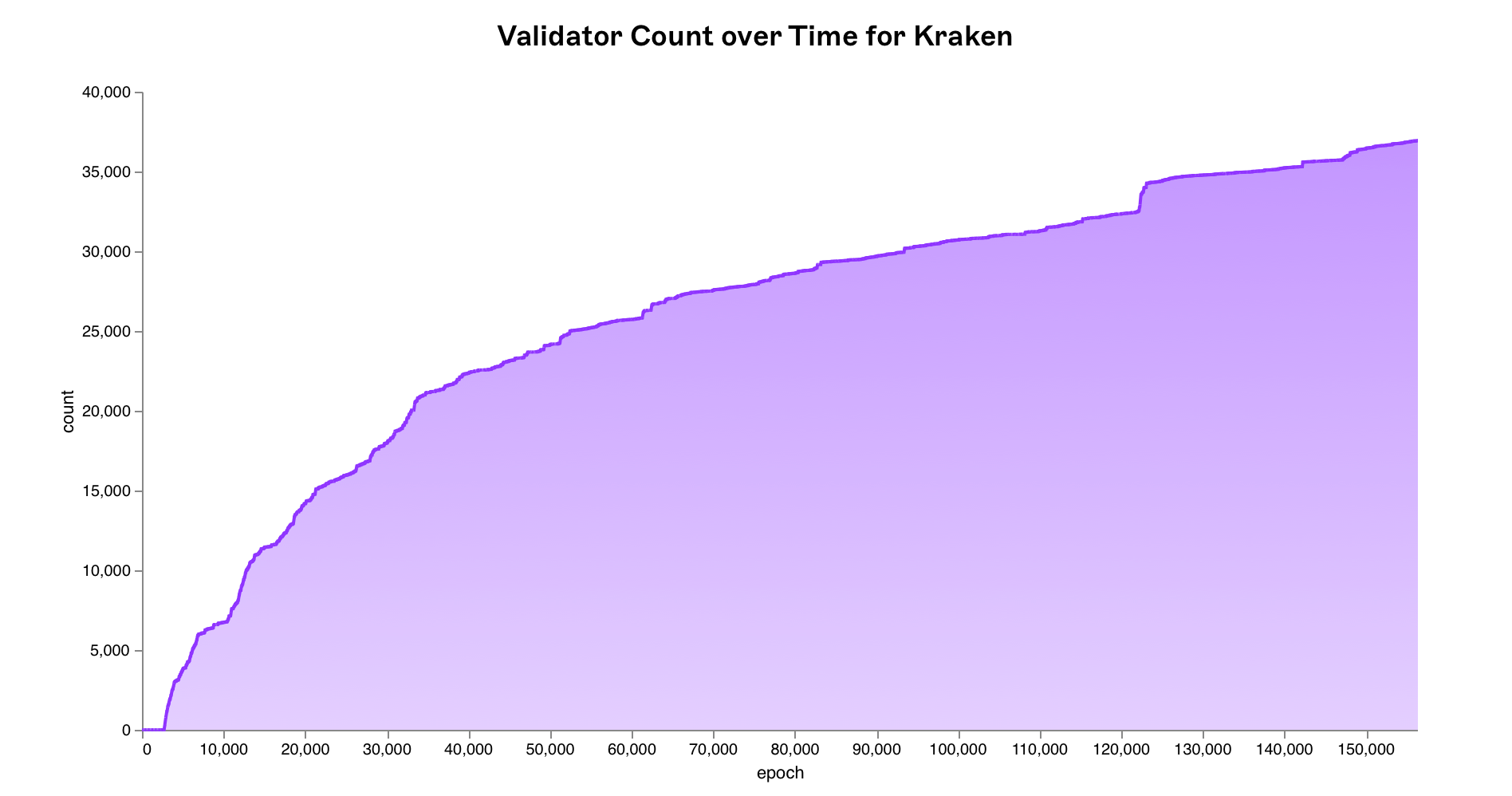 In tracking all deposits made from Kraken’s depositor address, we can attribute validator public keys to this entity. This can be achieved by looking at
In tracking all deposits made from Kraken’s depositor address, we can attribute validator public keys to this entity. This can be achieved by looking at DepositEvent logs from the beacon deposit contract and filtering transactions by the from field. It should be noted that although we have cross-referenced our own data with public sources including beaconcha.in and etherscan, it is possible that there are additional validators that have not been attributed to Kraken - as such this should be considered the lower bound.
There are 451,084 active validators on the beacon chain as of 22:33:59 UTC 26/10/2022 (epoch 156,249) with the majority concentrated in validator pools. Using the methodology described above, an estimated 36,922 validators or 8.1852% of the total network is attributed to Kraken.
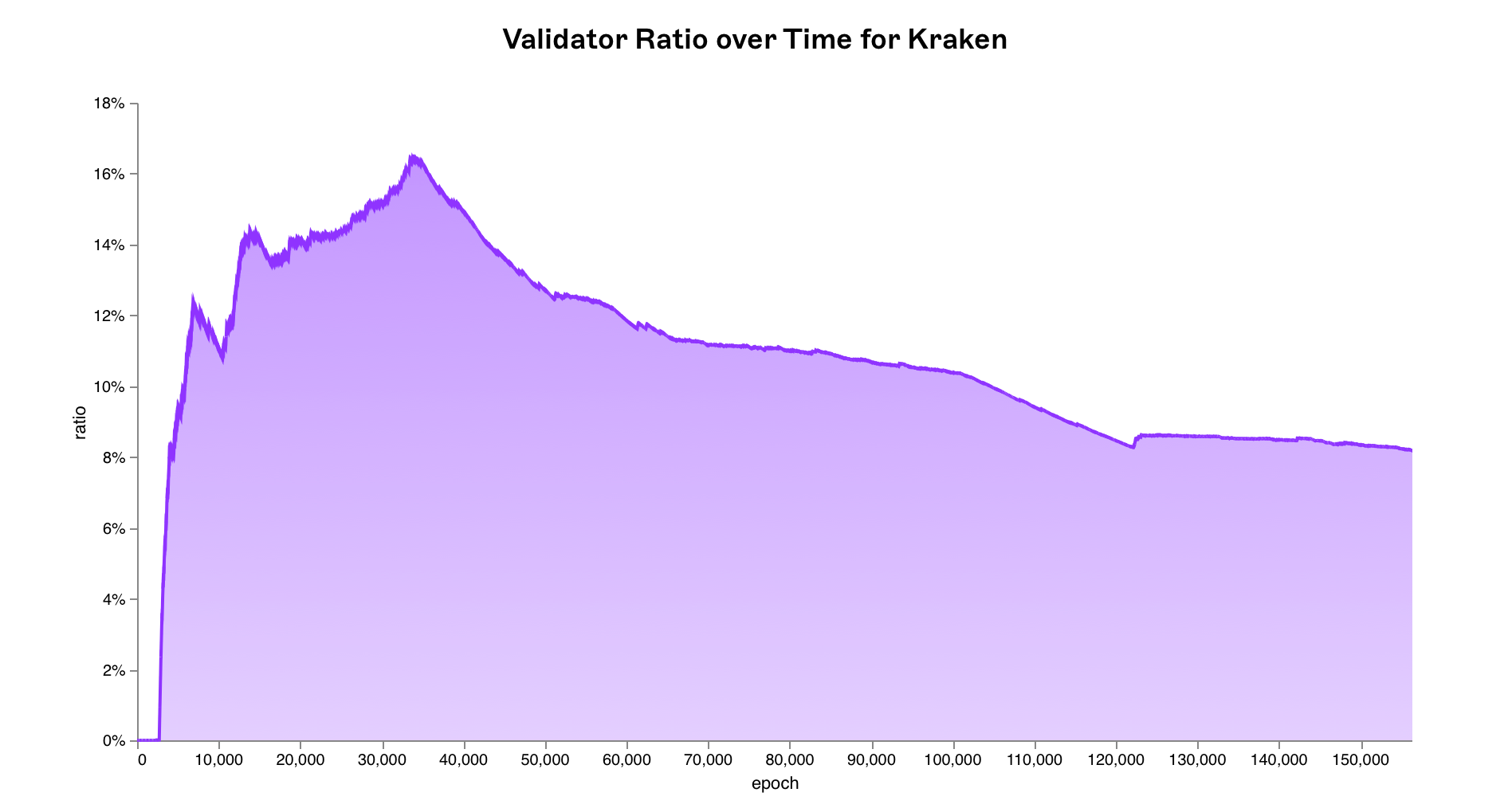 New validators can enter and exit the active validator set at every epoch i.e. new validators controlled by Kraken and other entities
New validators can enter and exit the active validator set at every epoch i.e. new validators controlled by Kraken and other entities activation_epoch as well as validators being forced to exit the network due to slashing exit_epoch. This needs to be reflected within our simulation. Therefore we update the validator ratios at every epoch using historical data from the beacon chain and run our simulation over 100,000 times per epoch for 156,250 epochs (all epochs since the beacon chain’s genesis) for a total of 15.625 billion simulated epochs.
Results
Whilst these real world events are simply one realisation of the probability distribution, the realised results very closely match our simulated/expected values.
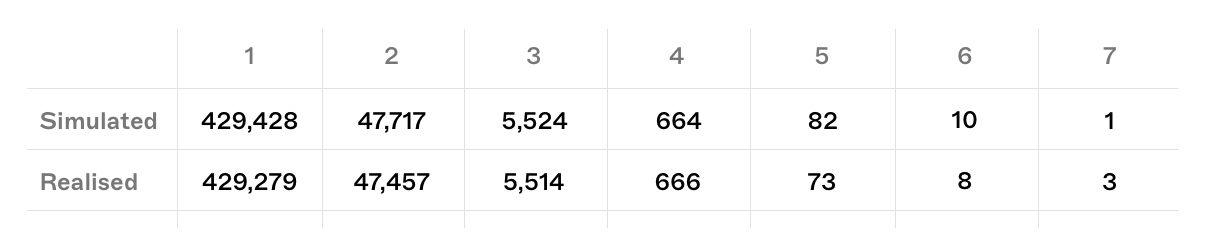 simulated vs realised k-blocktuple events since the beacon chain's genesis
simulated vs realised k-blocktuple events since the beacon chain's genesis
Three 7-blocktuple events occurred in early epochs when Kraken's validator ratio was nearing its peak. However, the most recent noteworthy run of 6 consecutive blocks occurred on recently on 18/10/22 during Epoch 154314, (slots 4,938,067 to 4,938,072).
Discussion
As can be seen from the empirical data, it is not uncommon for a validator pool with a large stake to propose 3 or more consecutive blocks. It should be noted that this should be considered the lower bound as we have only looked at k-blocktuples within epochs not across epochs. For example it is possible that a validator could have both slot 32 in epoch and slot 1 in epoch .
Additionally, the number of multiblock MEV opportunities is not proportional to the amount of ETH staked - rather it is skewed towards larger values of . At a certain point, the revenue from these opportunities might become sizable enough such that it is significantly more profitable to join a validator pool than to operate a solo validator - centralising the network.
An exhaustive study of all possible MEV strategies and attack vectors made possible by this e.g. arbitrage, oracle censoring is beyond the scope of this article. However it can help to highlight a couple of known risks and mitigations in order to contextualise the issue.
TWAP Oracle Manipulation
Many smart contracts today rely on the information supplied by price oracles to determine the value of certain assets. Uniswap’s V2 (arithmetic mean) and V3 (geometric mean) oracles are used by various lending protocols to determine borrow and collateral amounts and trigger liquidations. As the name suggests, these oracles provide a time weighted average price from a specified Uniswap pool to consumer smart contracts. By manipulating the price oracle, an attacker could trigger a series of liquidations or borrow more than they otherwise could, creating bad debt. Whilst there have been a number of TWAP manipulation exploits in the past, these are due to mistakes in their implementation.
The notion that TWAP oracles are robust is predicated on the assumption that multi-block manipulation of asset prices on AMMs is prohibitively expensive. However in a scenario where a malicious validator is able to propose multiple consecutive blocks, the cost and risk associated with such an attack is significantly reduced.
A nefarious actor could manipulate the price of either the collateral asset (down) or loan asset (up) on an AMM pool as part of a liquidation strategy. A lending protocol using the TWAP as a price oracle, would assume that certain debt positions are undercollateralised and put them up for liquidation. The attacker would then submit their own transactions to capture the liquidation bonus.
In order to prevent intra-block manipulations with flashloans, most TWAP oracles include the last traded price/tick from the previous block at block . This means the price manipulation must span at least 1 block. Such a large price dislocation would result in a highly lucrative arbitrage opportunity visible to everyone on the network.
In a world where no consecutive blocks are proposed by the same or co-operating entities, there are no guarantees that an attacker will have control over the ordering of transactions in the next block. It follows that the attacker has no assurances that they will be the one to close the arbitrage and is therefore at risk of making a substantial loss. The loss incurred from this usually exceeds any potential gain the attacker stands to make - this served as a deterrent against such attacks. This is no longer the case with consecutive blocks where control over ordering is guaranteed meaning the cost of attack is effectively reduced to the pool's trading fees.
Mitigating against these multi-block TWAP manipulations is possible. For example, using a TWMP (time-weighted median price) oracle would require an attacker to sustain the price manipulation over significantly more blocks in order to achieve an equivalent target reported price. This does come at the expense of ‘freshness’ as TWMPs will be slower to start responding to price changes. In addition, the liquidity distribution within a V3 pool can dramatically change the cost of manipulation - by tactically placing out of range or wide-band liquidity, the cost of attack can be made to be significantly more expensive.
In light of these developments, some protocols have reduced or eliminated their reliance on TWAP oracles for the time being, instead aggregating prices from multiple sources themselves or using an m-of-n oracle. This however is not an option for the long tail of assets which typically have but a single DEX liquidity pool for price discovery. Additionally, a malicious validator could use a large k-blocktuple opportunity to censor any price oracle updates for an extended period of time (5 slots = 60s), preventing liquidations or contracts from settling at the correct price. Decentralised price oracles are an important piece of infrastructure, research into improving their robustness is both interesting and necessary.
RANDAO Biasability
The RANDAO value set at the end of epoch is used to pseudo-randomly assign the proposer and committee assignments in the epoch . The primary source of entropy for the RANDAO mix is the BLS signatures generated by block proposers. During the last slot of an epoch, a validator is able to prevent further changes to the RANDAO value - if advantageous to do so - by withholding blocks (or launching a DoS attack on the last validator since they are known ahead of time). Therefore a validator (or a colluding set of validators) proposing the last block(s) of epoch has some degree of influence over the final RANDAO mix. A validators’ influence over this grows with an exponentially increasing number of choices where 2 is the choice to propose or withhold a block and is the number of consecutive blocks they can propose at the end of an epoch.
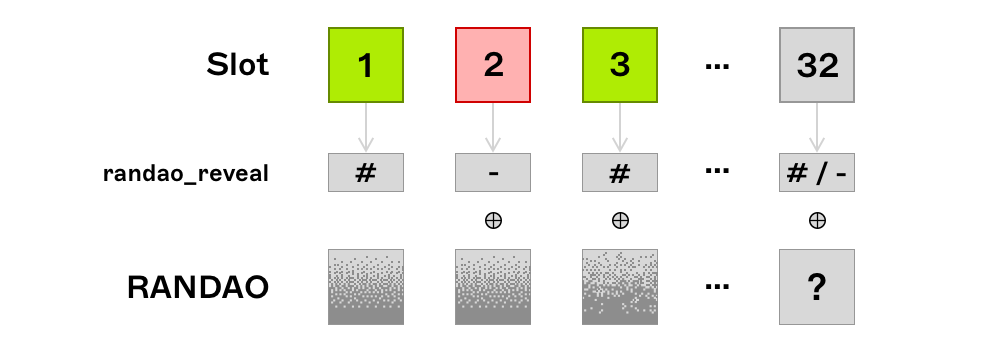
Although the RANDAO is biasable, the resulting randomness is ‘good enough’ for the security of the protocol. Of course true on-chain randomness cannot be generated since the EVM is deterministic. However, applications that utilise the RANDAO mix as a source of randomness PREVRANDAO should be designed such that any future randomness relied on is with a sufficiently high lookahead - preventing a motivated and well resourced attacker from leveraging their ability to predict the mix sooner than they otherwise should. Passing the RANDAO mix through a VDF would remove the possibility for opportunistic biassing but this is yet to be implemented.
DoS Attacks
Consider a scenario where Validator A has two 2-slot opportunities with 1 slot in between during which Validator B, an unrelated entity, is proposing a block. As mentioned earlier, validator public keys (identities) are known ahead of time. If Validator A is able to identify Validator B's IP address, they could launch a denial of service (DoS) attack to take down Validator B’s node until they have missed their slot. Validator A stands to gain a lot if they are able to successfully execute this attack: not only could they capture the transaction fees and MEV, but they could potentially use this attack to create a window where they are effectively proposing 4 consecutive blocks (by preventing a block from being proposed in between).
Conclusion
Consecutive blocks proposals by the same entity on Ethereum are expected and multiblock MEV can be a centralising force. Having validated our numerical solution and observed on-chain events, it is clear that multiblock MEV opportunities are common and to be expected. We are yet to discuss how PBS or SSLE could prevent some of these negative outcomes.
We will be building on this work in future pieces but do reach out if you want to work on something together! You can reach us by email ahmad@numeus.xyz and furkan@numeus.xyz.



